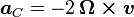Chris Peterson wrote:neufer wrote:
An accelerometer moving in an inertial frame of reference must detect zero acceleration so the guy starting free fall comes the closest to being in an inertial frame but technically it is not applicable:
Actually, it's a little more complicated than that. When you're comparing two frames, you can use special relativity to perform transforms between them when an accelerometer in each frame reads the same. They do not need to read zero. So in the case of the falling climber and the mountain, special relativity is applicable once terminal velocity is reached, and each experiences 1G towards the center of the Earth. Even though the neither frame is an inertial one, they are inertial with respect to one another.
- In an event, what I find interesting here is that
we are dealing with a clockwise rotating frame of reference (vis-a-vis the stars)
where: Ω = 2π cos(Lat)/86400 ~5.75 x 10-5
neufer wrote:
Assuming that the 3000' granite face of El Capitan was perfectly vertical and there was absolutely no wind
how would these objects land to the East (from Coriolis forces) after being dropped from the very top:
1) a cannonball?
2) a feather with low terminal velocity V?
1) The cannonball case is a simple case where the top of El Capitan
is moving eastward with respect to the base by ΩH ~ 2 inches per second.
The cannonball drops for sqrt(2H/g) ~ 13.7 seconds
by which time the cannonball has traveled about 28 inches to the East.
2) The feather is even simpler in that the Coriolis acceleration to the east = 2ΩV
makes a constant angle θ to the vertical acceleration g: tan(θ) = 2ΩV/g
The total eastward displacement (on average) is then H tan(θ) = 2ΩVH/g
~ 0.13 inches times V (where V the is feather's velocity in feet/second).
 Star Trails over El Capitan
Star Trails over El Capitan