Nitpicker wrote:Neufer, that strikes me as a rather obfuscated explanation. (At least I know it is really you.)
Assuming a planet is only orbiting one star, and assuming the only significant components to the analemma are eccentricity and axial tilt:
4) A planet with an eccentric orbit and some axial tilt, will have an analemma which may or may not cross itself (oval, teardrop, peanut, or figure-8 shaped), depending on whether the component of eccentricity is dominant enough to overcome the cross-over inherent in the tilt component.
Well, I can't help much with Art's interpretation but it may not be in conflict with your statements. It seems he is relating analemma crossing to EOT derivatives. I don't think he's disagreeing with you that eccentricity does affect crossing. In fact he'd quickly say that the crossing shares a coupled dependence between e and ε. However, I do find his discussion overly abstract. My contribution below is not easy to understand either, but you may find the result helpful.
Anyway, I decided to try to express analemma crossing mathematically in terms of the key parameters. This is not an easy problem. My reasoning was founded in an equivalence condition between EOT 1st and 2nd derivatives, but likely not related to Art's reasoning. By looking at the threshold condition for crossing in terms of the derivatives, I realized that one might be able to express an upper bound for crossing, i.e. given an axis tilt, the eccentricity must be < xxx for analemma crossing to occur. I soon remembered another significant factor that would have to be modeled. I call it Δ and it is defined as the angle between the Line of Apsides and the Line of Solstice (a similar line connecting the planet's summer and winter solstice orbital positions). Δ is a parameter that describes the apparent analemma tip. For Earth, if Δ = 0° then our "high noon" analemma would appear truly vertical (which it doesn't). Since the perihelion dates are ~13 days after the solstice, |Δ| ≈ 13°.
After some bona-fide derivation and brute force analysis, I derived a very good approximation for the upper bound eccentricity limit for analemma crossing. I only tested it for Earth and Mars having axis tilts (ε) ranging from 1° to ~70°, and Δ ranging from 0° to 65°. For all cases, the threshold eccentricity for crossing landed within 1% of the analemma models, and the predicted threshold eccentricity ranged from <0.0001 to ~3.3.
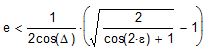
- Thresold Eccentricity for Analemma Crossing.JPG (10.44 KiB) Viewed 2372 times
I don't tout this to be a general solution for all conditions, but it is surprisingly accurate over a fairly broad test window. I haven't run across this relationship before and I'm probably the only one geeky enough to enjoy this find.
