| << Previous | Index | Next >> |
2015 Very faint but also very large on planet Earth's sky, a giant Squid Nebula cataloged as Ou4, and Sh2-129 also known as the Flying Bat Nebula, are both caught in this scene toward the royal constellation Cepheus. Composed with a total of 20 hours of broadband and narrowband data, the telescopic field of view is almost 4 degrees or 8 Full Moons across. Discovered in 2011 by French astro-imager Nicolas Outters, the Squid Nebula's alluring bipolar shape is distinguished here by the telltale blue-green emission from doubly ionized oxygen atoms. Though apparently completely surrounded by the reddish hydrogen emission region Sh2-129, the true distance and nature of the Squid Nebula have been difficult to determine. Still, a recent investigation suggests Ou4 really does lie within Sh2-129 some 2,300 light-years away. Consistent with that scenario, Ou4 would represent a spectacular outflow driven by a triple system of hot, massive stars, cataloged as HR8119, seen near the center of the nebula. If so, the truly giant Squid Nebula would physically be nearly 50 light-years across.
2014
[imghover6=http://apod.nasa.gov/apod/image/1409/be ... gmt900.jpg]http://apod.nasa.gov/apod/image/1409/be ... labels.jpg[/imghover6]Image Credit & Copyright: Yuri Beletsky (Las Campanas Observatory, Carnegie Institution)
2013 On September 6, a starry night and the Milky Way witnessed the launch of a Minotaur V rocket from NASA's Wallops Flight Facility on Wallops Island, Virginia. So did a large part of the eastern United States, as the spectacular night launch was easily visible even from light polluted urban areas. This 35 second exposure captures part of the rocket's initial launch streak and 2nd stage ignition flare along with a fiery reflection in calm waters. The stunning view faces south and west from a vantage point overlooking Sinepuxent Bay in Maryland about 20 miles north of the launch pad. Heading east over the Atlantic, the multi-stage rocket placed LADEE, the Lunar Atmosphere and Dust Environment Explorer, into a highly elliptical Earth orbit to begin its journey to the Moon.
2012 Which part of this picture do you find more interesting -- the land or the sky? Advocates for the land might cite the beauty of the ancient domes of the Bungle Bungle Range in Western Australia. These picturesque domes appear as huge layered beehives and are made of sandstones and conglomerates deposited over 350 million years ago. Advocates for the sky might laud the beauty of the Milky Way's central band shown arching from horizon to horizon. The photogenic Milky Way band formed over 10 billion years ago and now includes many well-known nebulae and bright stars. Fortunately, you don't have to decide and can enjoy both together in this beautiful 8-frame panorama taken from the dark skies of Purnululu National Park about two months ago.
2011 Where did the gold in your jewelry originate? No one is completely sure. The relative average abundance in our Solar System appears higher than can be made in the early universe, in stars, and even in typical supernova explosions. Some astronomers have recently suggested that neutron-rich heavy elements such as gold might be most easily made in rare neutron-rich explosions such as the collision of neutron stars. Pictured above is an artist's illustration depicting two neutron stars spiraling in toward each other, just before they collide. Since neutron star collisions are also suggested as the origin of short duration gamma-ray bursts, it is possible that you already own a souvenir from one of the most powerful explosions in the universe.
2010
2009 The first identified compact galaxy group, Stephan's Quintet is featured in this stunning image from the newly upgraded Hubble Space Telescope. About 300 million light-years away, only four galaxies of the group are actually locked in a cosmic dance of repeated close encounters. The odd man out is easy to spot, though. The four interacting galaxies (NGC 7319, 7318A, 7318B, and 7317) have an overall yellowish cast and tend to have distorted loops and tails, grown under the influence of disruptive gravitational tides. But the bluish galaxy at the upper left (NGC 7320) is much closer than the others. A mere 40 million light-years distant, it isn't part of the interacting group. In fact, individual stars in the foreground galaxy can be seen in the sharp Hubble image, hinting that it is much closer than the others. Stephan's Quintet lies within the boundaries of the high flying constellation Pegasus.
2008
2007 If Scorpius looked this good to the unaided eye, humans might remember it better. Scorpius more typically appears as a few bright stars in a well known but rarely pointed out zodiacal constellation. To get a spectacular image like this, though, one needs a good camera, color filters, and a digital image processor. To bring out detail, the above image not only involved long duration exposures taken in several colors, but one exposure in a very specific red color emitted by hydrogen that brings out great detail. The resulting image shows many breathtaking features. Vertically across the image left is part of the plane of our Milky Way Galaxy. Visible there are vast clouds of bright stars and long filaments of dark dust. Jutting out diagonally from the Milky Way in the image center are dark dust bands known as the Dark River. This river connects to several bright stars on the right that are part of Scorpius' head and claws, and include the bright star Antares. Above and right of Antares is an even brighter planet Jupiter. Numerous red emission nebulas and blue reflection nebulas are visible throughout the image. Scorpius appears prominently in southern skies after sunset during the middle of the year.
2006 Last Thursday, part of our Moon turned dark. The cause, this time, was not a partial lunar phase -- the Moon was full -- but rather that part of the Moon went into Earth's shadow. The resulting partial lunar eclipse was visible from the eastern Atlantic Ocean through Europe, Africa, and Asia and into the western Pacific Ocean. The darkest part of the lunar eclipse, when part of the Moon was completely shielded from sunlight, lasted about 90 minutes. Pictured above, a partially eclipsed Moon is seen rising over an estate in Huddersfield, England. The above image was taken far away from the house in the foreground, as only this would allow it to appear as angularly small as the half-degree Moon far in the background. A setting twilight Sun lit the foreground. The next eclipse of the Moon will occur in March 2007.
2005 Gas giant Jupiter is the solar system's largest world with about 320 times the mass of planet Earth. Famous for its Great Red Spot, Jupiter is also known for its regular, equatorial cloud bands, visible in very modest sized telescopes. The dark belts and light-colored zones of Jupiter's cloud bands are organized by planet girdling winds which reach speeds of up to 500 kilometers per hour. On toward the Jovian poles though, the cloud structures become more mottled and convoluted until, as in this Cassini spacecraft mosaic of Jupiter, the planet's polar region begins to look something like a brain! This striking equator-to-pole change in cloud patterns is not presently understood but may be due in part to the effect of Jupiter's rapid rotation or to convection vortices generated at high latitudes by the massive planet's internal heat loss. The Cassini spacecraft captured this dramatically detailed view of Jupiter in 2000 December during its turn of the millennium flyby enroute to Saturn.
2004 The night had no moon, but the stars were out. And camped at 16,000 feet on Mt. Kilimanjaro, photographer Dan Heller recorded this marvelous 3 1/2 hour long exposure. Here the landscape is lit mostly by the stars. Flashlights give the tents an erie internal radiance while the greenish glow from the distant city lights of Moshi, Tanzania filter through the clouds below. The view from this famous equatorial African mountain is toward the south, putting the South Celestial Pole close to the horizon on the far left, near the center of the graceful concentric star trail arcs. In the thin air and clear dark skies, even the ghostly Milky Way left a faint triangular glow as it swept across the middle of the dreamlike scene.
2003 Similar in size and grand design to our own Milky Way, spiral galaxy NGC 3370 lies about 100 million light-years away toward the constellation Leo. Recorded here in exquisite detail by the Hubble Space Telescope's Advanced Camera for Surveys, the big, beautiful face-on spiral does steal the show, but the sharp image also reveals an impressive array of background galaxies in the field, strewn across the more distant Universe. Looking within NGC 3370, the image data has proved sharp enough to study individual pulsating stars known as Cepheids which can be used to accurately determine this galaxy's distance. NGC 3370 was chosen for this study because in 1994 the spiral galaxy was also home to a well studied stellar explosion -- a type Ia supernova. Combining the known distance to this standard candle supernova, based on the Cepheid measurements, with observations of supernovae at even greater distances, can reveal the size and expansion rate of the Universe itself.
2002 Occasionally, a planet in our Solar System will pass in front of a bright star. Since stars and planets take up so little space on the sky, such events are quite rare. Two months ago, however, Pluto and its large moon Charon passed in front of a comparatively bright triple star system known as P126. By noting how P126 A dimmed, the event was useful for studying Pluto's relatively unknown atmosphere. A Very Large Telescope in Chile using a deformable mirror to counter the blurring effect of Earth's atmosphere captured the above image.
2001 The party is still going on in spiral galaxy NGC 3310. Roughly 100 million years ago, NGC 3310 likely collided with a smaller galaxy causing the large spiral galaxy to light up with a tremendous burst of star formation. The changing gravity during the collision created density waves that compressed existing clouds of gas and triggered the star-forming party. The above image composite by the Hubble Space Telescope was used to find the ages of many of the resulting clusters of stars. To the surprise of many, some of the clusters are quite young, indicating that starburst galaxies may remain in star-burst mode for quite some time. NGC 3310 spans about 50,000 light years, lies about 50 million light years away, and is visible with a small telescope towards the constellation of Ursa Major.
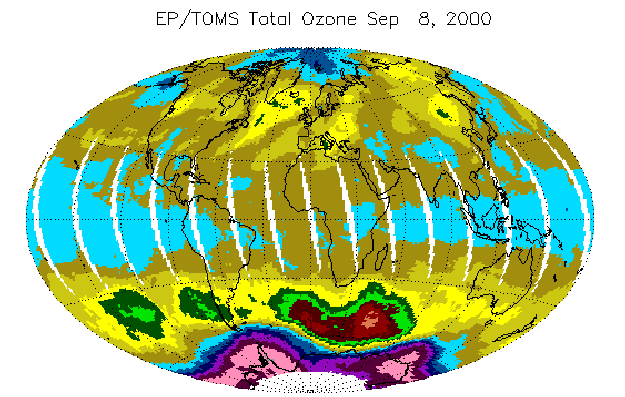
2000 It's back, and it's bigger than ever. The ozone hole that has been a cause of concern in recent years has again reformed over Earth's South Pole. The seasonal recurrence of the ozone hole was expected, although the size of the hole has never been so large this early in the season. Ozone is important because it shields us from damaging ultraviolet sunlight. Ozone is vulnerable, though, to CFCs and halons being released into the atmosphere. The ozone hole's large size is probably related to unusually low temperatures, allowing CFC byproducts like chlorine to react with atmospheric ozone molecules with greater efficiency. In the above false-color picture taken earlier this month, low ozone levels are shown in red and grey.
1999 The sky toward the center of our Galaxy is filled with a wide variety of celestial wonders. Many are easily visible with binoculars. Constellations near the galactic center include Sagittarius, Libra, Scorpius, Scutum, and Ophiuchus. Nebulae include Messier Objects M8, M16, M17, M20 and the Pipe Nebula. Open star clusters include M6, M7, M18, M21, M23, M24, M25. Globular star clusters include M9, M22, M28, M54, M69, M70. And don't forget Baade's Window. Click on the photo to get the un-annotated version.
1998 You can help map the Moon. Early tomorrow morning (Saturday, September 12) the Moon will occult, or pass in front of, the bright star Aldebaran as viewed from some Southern and Eastern areas of the U.S. as well as regions in the Caribbean Sea, Nova Scotia, Newfoundland, Mexico, and Central America. Aldebaran will disappear behind the bright edge of the third quarter moon and reappear behind the darkened edge. Accurately timed home video camera recordings from different locations can be used to make improved maps of the height of the lunar terrain at these occultation points. Interested? Follow the instructions on the International Occultation Timing Association HomePage which detail how to tape a familiar TV channel, take your running camcorder outside to record the occultation, and then return to tape a few more minutes of the TV channel. (First, determine if the occultation will be visible from your location!) You can then donate your tape by mailing it to the address given. Leave yourself plenty of time for a practice run and be sure to check the weather before going to a lot of trouble!
This mosaic mapping the North polar region of the lunar surface was constructed from images recorded by the Galileo spacecraft in 1992.
1997 Completing a 10 month journey, another spacecraft from Earth arrives at Mars today. The Mars Global Surveyor (MGS) is scheduled to fire its main rocket engine for 22 minutes at 6:17 p.m. PDT and enter a highly elliptical orbit, with a low point 186 miles and a high point 34,800 miles above the surface of Mars. This robot spacecraft is aptly named. Its mission is to undertake a detailed planetwide survey of Mars. But first MGS must circularize its orbit, lowering the high point to about 250 miles. Instead of relying solely on its rocket engine, MGS mission controllers will use a fuel-saving technique known as aerobraking - dipping the spacecraft into the Martian atmosphere where it will encounter increased atmospheric drag. This early artist's conception emphasizes the drag created by the wing-like solar panels. The cumulative effect should find MGS in a more circular mapping orbit by March 1998. To successfully use aerobraking, mission controllers must achieve an exact orbit and will be handicapped by a limited knowledge of the thickness of the Martian atmosphere. They may even need to alter the spacecraft's course to compensate for changes in Martian weather.
1996 What is happening in the center of nearby spiral galaxy M77? To find out, astronomers used the Hubble Space Telescope to peer deep into the dusty chaos of this active galactic nucleus in 1994. They found a network of filamentary gas and opaque dust that provides only clues as to what central monster had left this mess. Due to the presence of hot ionized gas clouds near the core, changes in brightness that can take less than a week, and the ultraviolet halo surrounding the whole galaxy, the leading hypothesis is that a supermassive black hole lies at the center of this Seyfert Type 2 galaxy. Also known as NGC 1068, this galaxy lies only about 50 million light years distant and is visible with only a small telescope.
1995 The fuzzy blobs seen above may be some of the first ever images of entire solar systems forming right before our eyes. This close up of the Orion Nebulae taken by the Hubble Space Telescope shows only a few stars, but these stars are surrounded by proto-planetary disks known as "proplyds." As the stars have only just recently formed - in the past few million years - the disks around them are likely condensing to form planetary systems and may be similar to the disk that formed our own solar system 5 billion years ago. These HST results suggest that stars with planets may be relatively common place. Are there extra-terrestrial civilizations out there as well?
| << Previous | Index | Next >> |