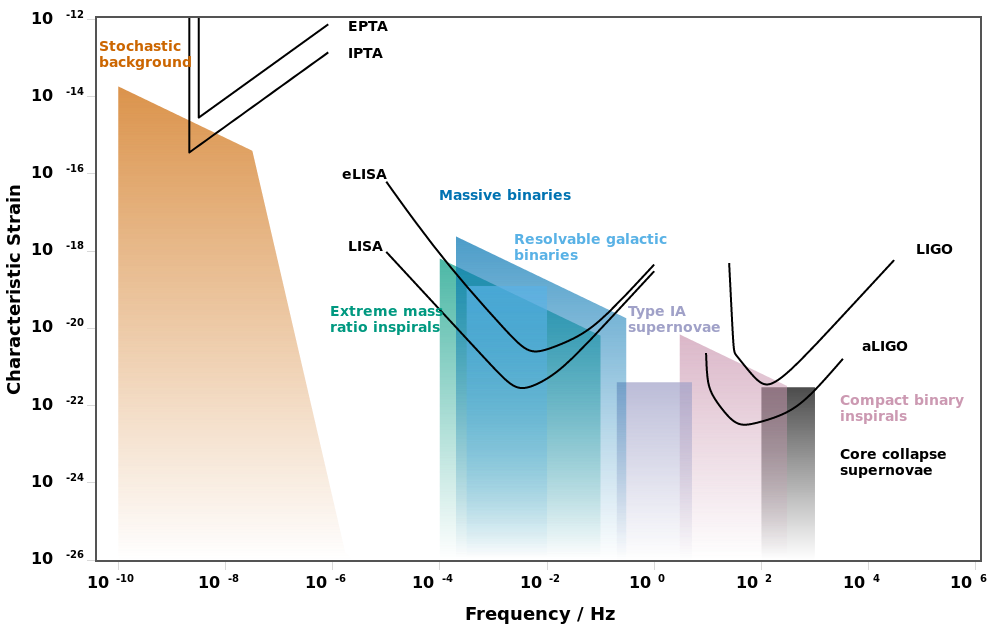
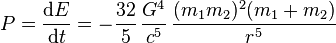MarkBour wrote:neufer wrote: . . .
- 1) Time to the first power
2) Mass squared
3) Frequency cubed and
4) Size to the fourth power.
. . .
Not to quibble, but would it be better to say "size to the
negative fourth power" ?
Actually, I have made an error

It should read:
- 1) Time to the first power
2) Mass squared
3) Size to the fourth power and
4) Frequency to the FIFTH power 
The
strong sensitivity to frequency dominates in a binary gravitational situations such a merging black holes since Kepler tells us that Frequency = "size to the
negative 3/2 power"
Allowing for this effect the graviton production = "size to the
negative 7/2 power" [= 4 - 5x(3/2)]
and the power P = "size to the
negative 5 power" as in the Wikipedia formula below.
(Note that each graviton has an increasing quantum energy = "size to the
negative 3/2 power")
https://en.wikipedia.org/wiki/Gravitational_wave wrote:
<<Suppose that [two orbiting masses] are m
1 and m
2, and they are separated by a distance r. The power given off (radiated) by this system is:
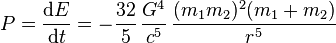
where G is the gravitational constant, c is the speed of light in vacuum and where the negative sign means that power is being given off by the system, rather than received. For a system like the Sun and Earth, r is about 1.5×10
11 m and m
1 and m
2 are about 2×10
30 and 6×10
24 kg respectively. In this case, the power is about 200 watts.>>
- So the Sun / Earth system radiates only about 200 watts or ~9.5x1042 gravitons per second.
But what if we substituted a
full sized orrery model with a Sun & Earth of masses 2000 kg & 6 g respectively?
-----------------------------------------------------------------------------------------
The power depends upon the masses squared and the masses have dropped by a factor of 10
27; hence the radiation drops by a factor of 10
54 resulting in a radiation of ~9.5x10
-12 gravitons per second or 3x10
-4 gravitons per year.
-----------------------------------------------------------------------------------------
Things get even worse if we make the orrery a
more feasible (1 AU => 150 m) size since gravitational radiation depends upon distances to the fourth power! Now our realistic yearly orrery puts out just 3x10
-32 gravitons per year. Clearly there is not enough time in the life of the universe for our realistic yearly orrery model to emit even a single graviton.
-----------------------------------------------------------------------------------------
Now what if we speed our realistic orrery model up to make an orbit in just one second? Now radiation depends upon frequency to the sixth power whereas graviton energy (= hv) only depends upon frequency to the first power such that graviton production increases as frequency to the fifth power.
Our realistic very fast orrery now puts out ~12 gravitons per hour.
-----------------------------------------------------------------------------------------
Hence...I concede that humans with masses 10
4 larger than the orrery's 6 g "Earth" (the main generator) but sizes 10
2 smaller than the orrery are capable of generating a few gravitons per hour on a good day.
However, heart pumping with blood masses 10
3 smaller and sizes 10
1 smaller will require 10
10 hours to produce a single graviton.
 Advanced LIGO: Gravitational Wave Detectors Upgraded
Advanced LIGO: Gravitational Wave Detectors Upgraded